政华公考

【答案】C【解析】本题中5个人包子总和固定为35，求分得包子最少的人分到的最大值，符合“和定最值”的特征。总量一定，要使数量最少的人包子数尽量大，那么其余人的包子数就要尽可能地小。根据这个思想，我们设分得包子数最少的人分了x个包子，由于每个人分得的包子数互不相同，则其他人的包子数要比x大，还要尽量小，那么可以分别设为x+1、x+2、x+3、x+4个。此时5个人的包子总数可以表示为(x+4)+(x+3)+(x+2)+(x+1)+x=35，得出x=5，即分得包子最少的人最多可以分到5个，所以本题选择C项。

2.解题原则

根据上面的题目，我们可以总结出和定最值问题的解题原则：当总量一定的情况下，若要求其中某个量的最大值，其他量应该尽可能小；若要求其中某个量的最小值，其他量应该尽可能大。解题方法可以设未知数，根据题目列方程求解。

3.方法应用

例题：某连锁企业在10个城市共有100家专卖店，每个城市的专卖店数量都不同。如果专卖店数量排名第五多的城市有12家专卖店，那么专卖店数量排名最后的城市，最多有几家专卖店？（）

A.2 B.3 C.4 D.5

【答案】C【解析】这道题中10个城市的专卖店之和为100，求解的是数量排名最后的城市，其专卖店数量最大值。此题就是前面讲的和定最值问题，所求解的是最小量的最大值。

根据和定最值问题的解题原则：若要求某个量为最大，其他量要尽量小。要排名最后的城市专卖店数量最多，那么其他城市专卖店数量要尽可能地少。题目中唯一确定量，就是数量第五多的城市有12家，如果数量第一多到第四多城市的专卖店数量要想尽量小，且数量不一样，还要比数量第五的城市大，那么就应该是16，15，14，13家；同理，数量第六多到数量排名第十一要尽量小，且都比数量排名最后的城市大，那么每个城市的专卖店数量尽可能地接近。根据这个思想，我们可以设数量排名最后的城市有x家专卖店，数量第六多到数量排名第九的城市可设为x+4、x+3、x+2、x+1。我们把10家城市的专卖店数量已经分别设置好未知数和常量，总和为100，故有：

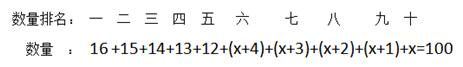
整理后求出x=4，所以本题选择C项。

相信通过以上的分析，大家对这类题型应该有了一定的了解，这类题型难度不大，只要掌握好解题原则，稍加练习，这类题型将是我们的易得分点。

行测备考：一起学习和定最值问题

在行测数量关系中，极值问题比较常见，极值就是求某个量的最大值或最小值，那么其中有一类常见题型为和定最值，对于这样的问题，掌握基本的题型特征和解题方法很重要。今天就给大家分享和定最值这个知识点。

知识点详解

1.题型特征：已知几个数的和一定，求其中某个数的最大值或最小值的问题。

2.解题原则：当总和一定的情况下，

若求其中某个数的最大值，则让其它数尽可能的小；

若求其中某个数的最小值，则让其它数尽可能的大。

解题方法：根据题目信息建立等量关系从而求解。

3.取整原则：求最大，向下取整；求最小，向上取整。

实战应用

例1：5名学生参加“最美逆行者”征文比赛，共得93分。已知每人得分各不相同且均为整数，且最低是13分，则最高分最高为？（）

A.30分 B.35分 C.40分 D.45分

【答案】B【解析】

由题目已知，每人得分各不相同，故可将5名学生按照成绩由大到小排序(如上图所示)，此时要求排名第一的学生分数最高，则使其他4名同学成绩尽可能的低。此时在表中标上相应的箭头(最高：向上箭头，最低：向下箭头)。已知最低为13分，且得分各不相同均为整数，那么其他人要想尽可能的低，则设第一名为X，则第五、四、三、二名依次应为13、14、15、16，共为93分，故有X+16+15+14+13=93，即X+58=93，解得X=35，故最高分最高为35分，选B项。

例2：2022年8月四川成都高温天气温度持续达到42度，某企业开展了爱心送水活动，现有100瓶冰水，把这些冰水送给10名环卫工人，每名环卫工人分得的数量都不相同，则分得最少的环卫工人至多分得多少瓶冰水？（）

A.3瓶 B.4瓶 C.5瓶 D.6瓶

【答案】C【解析】

由题目已知，每人分得的冰水数都不相同，故可将环卫工人按照分得水的瓶数由大到小排序(如上图所示)。依据解题原则，共有100瓶冰水分给环卫工人，分得最少的环卫工人(也就是第十名)要尽可能大，在其对应排名下标上“向上箭头”，那其余9名环卫工人就要尽可能小，在其对应排名下分别标上“向下箭头”。每名环卫工人分得的冰水数互不相等且为整数，而第一至第九名分得的水的最小值取决于最后一名，故设第十名环卫工人分得X瓶冰水，则第九名要想取到最小值就需要尽可能接近第十名并大于第十名，所以最少也要比第十名多1瓶，故第九名最小值为X+1，以此类推，第八名最小值为X+2，第七名最小值为X+3……，一共有100瓶冰水，由此可列：X+(X+1)+(X+2)+(X+3)+(X+4)+(X+5)+(X+6)+(X+7)+(X+8)+(X+9)=100，即10X+45=100，解得X=5.5，即第十名环卫工人最多是5.5瓶，那么冰水的数量不能比5.5更多，而瓶数必为整数，所以需要向下取整为5瓶。因此分得最少的环卫工人至多分得5瓶冰水，则选C项。

综上，大家会发现和定最值这个知识点较为简单且容易掌握，但一定要注意几个量之间是否相同以及取整原则，同学们还要通过多做题目达到举一反三的效果。

细说行测数量关系的“和定最值”

在行测数量关系考试中有一种解题思路相对固定同时比较容易掌握的题型——“和定最值”，接下来大家可以跟着一起学习，相信能对大家的备考有所帮助。

题型特征

几个数的和一定，求其中某个数的最大或最小值。

解题原则

几个数的和一定，若要求其中某一个数的最大值，则让其他数尽可能小；若要求某一个数的最小值，则让其他数尽可能大。

例1：5名学生参加某学科竞赛，共得91分，已知每人得分各不相同，且最高是21分，则最低分至少是：（）

A.14 B.16 C.13 D.15

【答案】C【解析】如下所示，将五名学生按照分数从高到低依次排列：

已知五人分数之和为91，所求为最低分即第五名的最小值，则让一至四名分数尽可能高，已知最高是21分，且每人分数各不相同，因此一至四名的分数取最大值依次为21，20，19，18。根据总分为21+20+19+18+X=91，解得X=13。选择C。

例2：现有21本故事书要分给5个人阅读，如果每个人得到的数量均不相同，那么得到故事书数量最多的人至少可以得到（）本。

A.5 B.7 C.9 D.11

【答案】B【解析】如下所示，将五个人按照所得故事书从多到少依次排列：

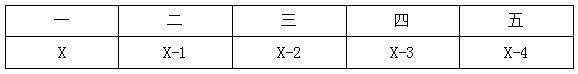
已知故事书总数为21本，所求为分得数量最多的人即一号的最小值，则让二、三、四、五号所取得的故事书尽可能多，不妨设一号的最小值为X，由于“每个人得到的数量均不相同”，此时二号尽可能多的同时也要略少于一号，因此二号最大取X-1，以此类推，三号、四号、五号的最大值依次为X-2、X-3、X-4。根据书本总数为X+X-1+X-2+X-3+X-4=21，解得X=6.2。因书本是整数且所求为最小值，故向上取整，X=7。选择B。

例3：10个箱子总重100公斤，且重量排在前三位的箱子总重不超过重量排在后三位的箱子总重的1.5倍。问最重的箱子重量最多是多少公斤？（）

A.200/11 B.500/23 C.20 D.25

【答案】B【解析】将十个箱子按照由重到轻的顺序从左往右依次排列，如下所示：

已知总重量为100公斤，所求为最重的箱子即一号箱子的最大值，则令二至十号箱子尽可能小，题中并未强调箱子的重量不能相同，因此我们假设二至十号箱子同时取最小值X。又因为“重量排在前三位的箱子总重不超过重量排在后三位的箱子总重的1.5倍”，而此时后三个箱子总重为3X，在一号箱子取最大值，而二、三号的重量都为X时，则一、二、三3个箱子的重量之和最大只能取4.5X，所以一号箱子最大为4.5X-X-X=2.5X，因此十个箱子总重量可表示为2.5X+9X=11.5X=100，解得X=200/23，故所求为2.5X=500/23，选择B。

通过以上三道题我们可以看到，和定最值问题的题型特征还是比较明显的，解题思路也相对比较固定，当然需要注意的例3相对于前两题来说，还是有一些区别的，它不同于前两题每一项都是整数，同时也没有要求各项均不相同，所以大家在实际做题当中还是要看清题目中的具体要求，灵活应变。